A modelagem mais moderna para a Teoria da Resposta ao Item utiliza a Estatística Bayesiana. Nessa modelagem, a probabilidade de acerto de um item é condicionada à habilidade e conhecimento do examinando. A curva que modela a probabilidade de acerto de um item é uma função crescente na ordenada da habilidade e conhecimento; o gráfico que tem a probabilidade condicional de acerto de um item na ordenada e a habilidade e conhecimento na abscissa é conhecido como Curva Característica do Item.
Na abordagem bayesiana da Teoria da Resposta ao Item costuma-se representar a habilidade e conhecimento por uma variável aleatória simbolizada pela letra grega  ; a variável aleatória que representa o acerto ou erro de um item ´s simbolizada pela letra
; a variável aleatória que representa o acerto ou erro de um item ´s simbolizada pela letra  ; o resultado (acerto ou erro) de um item respondido é representado por
; o resultado (acerto ou erro) de um item respondido é representado por  , onde
, onde  normalmente representa o acerto do item e
normalmente representa o acerto do item e  representa o erro. O gráfico da Curva Característica do Item acima é portanto um gráfico que associa a probabilidade de acerto
representa o erro. O gráfico da Curva Característica do Item acima é portanto um gráfico que associa a probabilidade de acerto  em função de
em função de  . Adicionalmente costuma-se utilizar o índice
. Adicionalmente costuma-se utilizar o índice  para indicar um examinando específico (
para indicar um examinando específico ( representa a habilidade e conhecimento do examinando
representa a habilidade e conhecimento do examinando  ) e o índice
) e o índice  para indicar um item específico (
para indicar um item específico (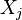 representa os possíveis resultados do item
representa os possíveis resultados do item  e
e  representa a resposta do examinando
representa a resposta do examinando  ao item
ao item  ).
).
 ; a variável aleatória que representa o acerto ou erro de um item ´s simbolizada pela letra
; a variável aleatória que representa o acerto ou erro de um item ´s simbolizada pela letra  ; o resultado (acerto ou erro) de um item respondido é representado por
; o resultado (acerto ou erro) de um item respondido é representado por  , onde
, onde  normalmente representa o acerto do item e
normalmente representa o acerto do item e  representa o erro. O gráfico da Curva Característica do Item acima é portanto um gráfico que associa a probabilidade de acerto
representa o erro. O gráfico da Curva Característica do Item acima é portanto um gráfico que associa a probabilidade de acerto  em função de
em função de  . Adicionalmente costuma-se utilizar o índice
. Adicionalmente costuma-se utilizar o índice  para indicar um examinando específico (
para indicar um examinando específico ( representa a habilidade e conhecimento do examinando
representa a habilidade e conhecimento do examinando  ) e o índice
) e o índice  para indicar um item específico (
para indicar um item específico (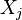 representa os possíveis resultados do item
representa os possíveis resultados do item  e
e  representa a resposta do examinando
representa a resposta do examinando  ao item
ao item  ).
).
Existe uma gama extensa de modelos da Teoria da Resposta ao Item: os modelos mais complexos podem considerar uma multidimensionalidade da habilidade e conhecimento onde a variável teta que a representa é um vetor multidimensional  como também considerar a abordagem de créditos parciais para acomodar itens com estágios hierárquicos de desenvolvimento, por exemplo: primeiro estágio se nada está correto na resolução do item (
como também considerar a abordagem de créditos parciais para acomodar itens com estágios hierárquicos de desenvolvimento, por exemplo: primeiro estágio se nada está correto na resolução do item ( ). segundo estágio se o item foi corretamente esquematizou o problema corretamente (
). segundo estágio se o item foi corretamente esquematizou o problema corretamente ( ); terceiro estágio se o desenvolvimento do raciocínio está correto (
); terceiro estágio se o desenvolvimento do raciocínio está correto ( ) e; quarto estágio se o item foi respondido corretamente na íntegra (
) e; quarto estágio se o item foi respondido corretamente na íntegra ( ). O modelo de créditos parciais, embora pouco utilizado, é adequado para questões discursivas.
). O modelo de créditos parciais, embora pouco utilizado, é adequado para questões discursivas.
 como também considerar a abordagem de créditos parciais para acomodar itens com estágios hierárquicos de desenvolvimento, por exemplo: primeiro estágio se nada está correto na resolução do item (
como também considerar a abordagem de créditos parciais para acomodar itens com estágios hierárquicos de desenvolvimento, por exemplo: primeiro estágio se nada está correto na resolução do item ( ). segundo estágio se o item foi corretamente esquematizou o problema corretamente (
). segundo estágio se o item foi corretamente esquematizou o problema corretamente ( ); terceiro estágio se o desenvolvimento do raciocínio está correto (
); terceiro estágio se o desenvolvimento do raciocínio está correto ( ) e; quarto estágio se o item foi respondido corretamente na íntegra (
) e; quarto estágio se o item foi respondido corretamente na íntegra ( ). O modelo de créditos parciais, embora pouco utilizado, é adequado para questões discursivas.
). O modelo de créditos parciais, embora pouco utilizado, é adequado para questões discursivas.
O modelo mais simples e usual da Teoria da Resposta ao Item considera itens dicotômicos (onde os possíveis resultados são acerto ou erro) e uma função logística para modelar a Curva Característica do Item:
Na modelagem bayesiana da Teoria da Resposta ao Item, conforme citado no início, diz-se que as respostas  onde
onde  é o número de itens respondidos pelo examinando
é o número de itens respondidos pelo examinando  estão correlacionadas através da habilidade e conhecimento
estão correlacionadas através da habilidade e conhecimento  do examinando. Se
do examinando. Se  fosse conhecido, as respostas
fosse conhecido, as respostas  seriam independentes estatisticamente. Essa abordagem costuma suscitar algumas confusões pois para o cálculo daverossimilhança utilizaremos o fato de que
seriam independentes estatisticamente. Essa abordagem costuma suscitar algumas confusões pois para o cálculo daverossimilhança utilizaremos o fato de que  ,
,  , ...,
, ...,  são independentes estatisticamente, ao passo que
são independentes estatisticamente, ao passo que  ,
,  , ...,
, ...,  são estatisticamente dependentes. Essa propriedade é conhecida como independência condicional e pode ser estudada em mais detalhes em artigo de De Finetti, B; por ora consideremos que se soubéssemos o verdadeiro valor da habilidade e conhecimento de um examinando as suas respostas a um conjunto de itens seriam estatisticamente independentes pois já saberíamos sua habilidade. Dessa forma, submetê-lo a um conjunto de itens seria inútil: os acertos e erros aos itens seriam meramente aleatórios. Para que a Teoria da Resposta ao Item seja aplicável é necessário pressupor que a habilidade e conhecimento de um examimando seja conhecido através de uma incerteza, representada por uma distribuição de probabilidade, e que os acertos e erros de um examinando numa prova revelem informações sobre seus conhecimentos e habilidades.
são estatisticamente dependentes. Essa propriedade é conhecida como independência condicional e pode ser estudada em mais detalhes em artigo de De Finetti, B; por ora consideremos que se soubéssemos o verdadeiro valor da habilidade e conhecimento de um examinando as suas respostas a um conjunto de itens seriam estatisticamente independentes pois já saberíamos sua habilidade. Dessa forma, submetê-lo a um conjunto de itens seria inútil: os acertos e erros aos itens seriam meramente aleatórios. Para que a Teoria da Resposta ao Item seja aplicável é necessário pressupor que a habilidade e conhecimento de um examimando seja conhecido através de uma incerteza, representada por uma distribuição de probabilidade, e que os acertos e erros de um examinando numa prova revelem informações sobre seus conhecimentos e habilidades.
 onde
onde  é o número de itens respondidos pelo examinando
é o número de itens respondidos pelo examinando  estão correlacionadas através da habilidade e conhecimento
estão correlacionadas através da habilidade e conhecimento  do examinando. Se
do examinando. Se  fosse conhecido, as respostas
fosse conhecido, as respostas  seriam independentes estatisticamente. Essa abordagem costuma suscitar algumas confusões pois para o cálculo daverossimilhança utilizaremos o fato de que
seriam independentes estatisticamente. Essa abordagem costuma suscitar algumas confusões pois para o cálculo daverossimilhança utilizaremos o fato de que  ,
,  , ...,
, ...,  são independentes estatisticamente, ao passo que
são independentes estatisticamente, ao passo que  ,
,  , ...,
, ...,  são estatisticamente dependentes. Essa propriedade é conhecida como independência condicional e pode ser estudada em mais detalhes em artigo de De Finetti, B; por ora consideremos que se soubéssemos o verdadeiro valor da habilidade e conhecimento de um examinando as suas respostas a um conjunto de itens seriam estatisticamente independentes pois já saberíamos sua habilidade. Dessa forma, submetê-lo a um conjunto de itens seria inútil: os acertos e erros aos itens seriam meramente aleatórios. Para que a Teoria da Resposta ao Item seja aplicável é necessário pressupor que a habilidade e conhecimento de um examimando seja conhecido através de uma incerteza, representada por uma distribuição de probabilidade, e que os acertos e erros de um examinando numa prova revelem informações sobre seus conhecimentos e habilidades.
são estatisticamente dependentes. Essa propriedade é conhecida como independência condicional e pode ser estudada em mais detalhes em artigo de De Finetti, B; por ora consideremos que se soubéssemos o verdadeiro valor da habilidade e conhecimento de um examinando as suas respostas a um conjunto de itens seriam estatisticamente independentes pois já saberíamos sua habilidade. Dessa forma, submetê-lo a um conjunto de itens seria inútil: os acertos e erros aos itens seriam meramente aleatórios. Para que a Teoria da Resposta ao Item seja aplicável é necessário pressupor que a habilidade e conhecimento de um examimando seja conhecido através de uma incerteza, representada por uma distribuição de probabilidade, e que os acertos e erros de um examinando numa prova revelem informações sobre seus conhecimentos e habilidades.
Considerando a propriedade da independência condicional dos acertos e erros dos itens respondidos por um examinando, a verossimilhança gerada pelas respostas de um examinando é dada por:
Após o examinando responder um conjunto de itens a estimativa da habilidade e conhecimento pode ser facilmente calculada através do Operador de Bayes:
Onde  é a distribuição de probabilidade a priori para a habilidade e conhecimento do examinando
é a distribuição de probabilidade a priori para a habilidade e conhecimento do examinando  , :
, : é a verossimilhança gerada pelas respostas aos itens e
é a verossimilhança gerada pelas respostas aos itens e  é a distribuição de probabilidade a posteriori para o mesmo examinando ao responder os itens
é a distribuição de probabilidade a posteriori para o mesmo examinando ao responder os itens  .
.
 é a distribuição de probabilidade a priori para a habilidade e conhecimento do examinando
é a distribuição de probabilidade a priori para a habilidade e conhecimento do examinando  , :
, : é a verossimilhança gerada pelas respostas aos itens e
é a verossimilhança gerada pelas respostas aos itens e  é a distribuição de probabilidade a posteriori para o mesmo examinando ao responder os itens
é a distribuição de probabilidade a posteriori para o mesmo examinando ao responder os itens  .
.



Nenhum comentário :
Postar um comentário
Obrigado ! Seu FEEDBACK é muito importante !